累乗とは,ある数を複数回かけることをいいます。例えば,
\( 2 × 2 \)
や
\( 3 ^ 4 \)
などは累乗といえます。累乗を冪乗(べきじょう)と表現することもありますが,最近の教科書では累乗に統一されているようです。累乗にはどんなきまりがあるのでしょうか?
累乗に関する計算のきまりを
指数法則
といいます。今回は,指数法則のいくつかを紹介して,皆さんに理解してもらおうと思います。
-
\( a ^ m × a ^ n = a ^ { m + n } \)
数式をみて意味がわかりますか? 実際に数字を入れて考えてみると,わかりやすくなるかもしれません。
\(
\begin{align*}
2 ^ 2 × 2 ^ 3 & = ( 2 × 2 ) × ( 2 × 2 × 2 ) \\
& = 2 × 2 × 2 × 2 × 2 \\
& = 2 ^ 5\\
つまり\\
2 ^ 2 × 2 ^ 3 & = 2 ^ { ( 2 + 3 ) } \\
& = 2 ^ 5
\end{align*}
\)
-
\( (a ^ m) ^ n = a^{mn} \)
この例についても,実際の数字で確認してみましょう。
\(
\begin{align*}
(2 ^ 2) ^ 3 & = ( 2 ^ 2 ) × ( 2 ^ 2 ) × ( 2 ^ 2 ) \\
& = (2 × 2) × (2 × 2) × (2 × 2)\\
& = 2 × 2 × 2 × 2 × 2 × 2\\
& = 2 ^ 6\\
つまり\\
(2 ^ 2) ^ 3 & = 2 ^ { ( 2 × 3 ) } \\
& = 2 ^ 6
\end{align*}
\)
-
\( (a ^ m) ÷ (a^n) = a^{m-n} \)
\(
\begin{align*}
(2 ^ 3) ÷ (2^2) & = ( 2 × 2 × 2 ) ÷ ( 2 × 2 ) \\
& = \frac{( 2 × 2 × 2 )}{( 2 × 2 )}\\
& = 2\\
つまり\\
(2 ^ 3) ÷ (2^2) & = 2 ^ { ( 3 - 2 ) } \\
& = 2 ^ 1\\
& = 2
\end{align*}
\)
-
\( (ab)^m = a^m b^m \)
この例については,自分で考えてみましょう。
何かの数字の0乗を計算することはできるのでしょうか? 実は,指数法則が常に成り立つとすると,0乗を計算できるのです。次の計算式を見てください。
\(
\begin{align*}
a^m × a^n & = a^{m+n}\\
なので\\
a^{m+n} & = a^m × a^n\\
\end{align*}
\)
m=0,n=1を代入し,両辺を整理します。
\(
\begin{align*}
a^{0+1} & = a^0 × a^1\\
a^1 & = a^0 × a^1\\
a & = a^0 × a
\end{align*}
\)
上の等式が成り立つためには,\(a^0\)が1でなくてはなりません。ですから,指数法則が常に成り立つとすると,\(a^0\)は1なのです。
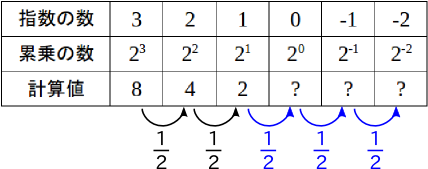
aにはどんな数字を入れてもよいのですから,\(2^0も15^0 \)も1ということになります。数式では納得できない人のために,表を使って,累乗の規則性を考えてみましょう。次の表を見てください。
指数の数を1ずつ小さくしていくと,計算値は\(\frac{1}{a}\)になっていきます。この規則にしたがうと,\(2^0\)は1, \(2^{(-1)}\)は\(\frac{1}{2}\), \(2^{(-2)}\)は\(\frac{1}{2^2}\)となります。
次の式を簡単な(累乗の)式に書きかえなさい。
- \( 5^3 × 5^{10} \)
- \( {(5^3)}^{10} \)
- \( 5^3 + 5^3 + 5^3 \)
- \( 987654321^0 \)
- \( 7^{(-2)} × 7^5 \)
今回のテーマはわかりにくいと思いますので,課題がしっかりできた時点で,銀メダルとします。